Si en un triángulo se traza una línea paralela a cualquiera de sus lados, se obtiene un triángulo que es semejante al triángulo dado. (fuente: wikipedia)
Según la leyenda (relatada por Plutarco1 ), Tales de Mileto en un viaje a Egipto, visitó las pirámides de Guiza (las de Keops, Kefrén y Micerino), construidas varios siglos antes. Admirado ante tan portentosos monumentos de esta civilización, quiso saber su altura. De acuerdo a la leyenda, trató este problema con semejanza de triángulos (y bajo la suposición de que los rayos solares incidentes eran paralelos), pudo establecer una relación de semejanza entre dos triángulos rectángulos, por un lado el que tiene por catetos (C y D) a la longitud de la sombra de la pirámide (conocible) y la longitud de su altura (desconocida), y por otro lado, valiéndose de una vara (clavada en el suelo de modo perfectamente vertical) cuyos catetos conocibles (A y B) son, la longitud de la vara y la longitud de su sombra. Realizando las mediciones en una hora del día en que la sombra de la vara sea perpendicular a la base de la cara desde la cual medía la sombra de la pirámide y agregando a su sombra la mitad de la longitud de una de las caras, obtenía la longitud total C de la sombra de la pirámide hasta el centro de la misma.
Como en triángulos semejantes, se cumple que 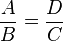 , por lo tanto la altura de la pirámide es
, por lo tanto la altura de la pirámide es 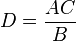 , con lo cual resolvió el problema.
, con lo cual resolvió el problema.
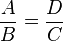 , por lo tanto la altura de la pirámide es
, por lo tanto la altura de la pirámide es 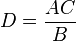 , con lo cual resolvió el problema.
, con lo cual resolvió el problema.



